速力及び馬力計算書(SPEED AND POWER CALCULATION)
以下に一般的な手計算での手法を冨田氏の船舶基本設計論より引用するが、実際には既にプログラム化されているので
そのプログラムより算出されるのが一般的である。
・馬力計算(Power Estimation)
船の馬力計算の過程は、まず船体抵抗値の算定と推進効率の推定とである。
実船の馬力推定は、計画船模型の曳航試験から抵抗値を、また、推進効率要素を自航試験から求め、実船実績の解析から得られた十分な修正項資料を加味して推定するのがより信頼性ある方法であるが、ここでは、計画段階における迅速な馬力推定のための船型主要素からの計算法を対象とする。
本章関連の主要記号を以下にまとめておく。
L 垂線間長さ(m)
Lw 計画満載吃水線上の長さ(m)
B 型幅(m)
d 型吃水(m)
Cb 方形肥瘠係数=▽/L・B・d
CbF (場合により、満載状態のCbとして使用する)
Cp 柱形肥瘠係数=Cb/Cmidship
Cmidshp 中央断面係数
Cw 水線面積係数
lcb 長さ方向の浮力中心位置、船体中央からの距離をLの%で示す
中央より前方の場合を
(-),後方の場合を (+)とする
▽ 型排水容積(m3)=L・B・d・C
△ 型排水量(t)=1.025・▽
S 浸水表面積(m²)
Fn Froude 数=v/√Lg
v 船の速力 (m/s)
V 船の速力 (knots)
R 全抵抗(kg)
RF 摩擦抵抗(kg)
CF 摩擦抵抗係数=RF/(1/2)・ρ・S・v^2
γF 摩擦抵抗係数=RF/ρ・▽^(2/3)・v^2
RR 剩余抵抗(kg)
CR 剩余抵抗係数=RR/(1/2)・ρ・S・v^2
γR 剩余抵抗係数=RR/ρ・▽^(2/3)・v^2
Rw 造波抵抗(kg)
Cw 造波抵抗係数=Rw/(1/2)・ρ・S・v^2
γw 造波抵抗係数=Rw/ρ・▽^(2/3)・v^2
g 重力加速度=9.80
(m/s²)
ρ 流体の密度 海水: 104.51 (kg.s²/m²)
淡水:101.96(kg-s²/m²)
Rn Reynolds 数=v・L/ν≒4.34・L・V×10^5
ν 流体の動粘性係数
15°C において、海水: 1.187×10-5 (m²/s)
淡水:1.139×10-6 (m²/s)
△CF 粗度修正係数
γ 船尾肥大度係数=(B/L)/{1.3(1-Cb)-0.031・ιcb
γE 船首肥大度係数=(B/L)/{1.3(1-Cb)+0.031・ιcb}
K 形状(影響)係数
DF 推進器直径(m)
H 推進器ピッチ(m)
H/Dp ピッチ比
Z 推進器翼数
AE 展開面積(m²)
αE 展開面積比=AE/(π/4)・DF^2
bm 平均翼幅比=π・αE/2・Z(1-boss ratio)
N 每分回転数(1/min)
n 每秒回転数(1/s)
BTR 翼厚比(翼中心)
ω 伴流係数=(ν-νA)/ν
νA 推進器前進速度(m/s)=ν(1-ω)
VA 推進器前進速度(knots)=V(1-ω)
T 推進器推力(kg)
KT 推力係数=T/ρ・n²・ DP4
t 推力減少係数=(T-R)/T
Q 推進器トルク(kg・m)
KQ トルク係数=Q/ρ・n²・ DP^5
EHP 有効馬力(PS)=R・ν/75
DHP 伝達馬力(PS)=EHP/ηP
THP 推力馬力(PS)=T・νA/75=EHP/ηH
J 推進器前進係数=νA/n・DP, VA/N・DP
δ 直径係数=N・DP/VA
BP 馬力係数=N・(DHP)^1/2/VA^2.5
BU 馬力係数 =N・(THP)^1/2/VA^2.5
η 推進効率=ηH・ηO・ηR・ηT
ηP 準推進効率=ηH・ηO・ηR
ηH 船殼効率=(1-t)/(1-ω)
ηO 単独推進器効率=THP/DHP=J・ΚT/2π・ΚQ
ηB 船後推進器効率
ηR 推進器効率比=ηB/ηO
ηT 伝達効率=DHP/BHP, DHP/SHP
σ キャビテーション数=(p-e) /(1/2)・νA^2 or (p-e)/(1/2)・ρ・νO^2
P 推進器軸心における圧力
(kg/m²)
e 水の蒸気圧力(kg/m²)
νC 推進器の(0.7×半径)における合成速度(m/s)
=√(νA²+(0.7π・DP・n)²)
Cad アドミラルティ係数=△^(2/3)・V^3/PS
1. 抵抗(Resistance)
船体抵抗は大別して、摩擦抵抗と剰余抵抗,あるいは粘性抵抗と造波抵抗, 及び空気抵抗とに分けられるが、特殊形状のものを除き,空気抵抗は僅かであるため、抵抗算定は上記前二者を対象とするのが普通である。
なお、粘性抵抗とは、船体の浸水面積と同じ面積の平板の摩擦抵抗と、船体が3次元曲面であることによる平板の摩擦抵抗よりの増加分である形状抵抗及び表面の粗度による増加分の粗度抵抗との合計をいう。
水抵抗のうち、剰余抵抗あるいは造波抵抗は模型試験資料に基づいて推定される。しかし、摩擦抵抗は Reynolds 数の,また造波抵抗は
Froude 数の関数で異種のものであるため、模型試験から直接,実船抵抗値の算定は不可能で、実船値への換算過程においてもなお検討を要する要素もあり,実船馬力算定法の決定的なものはまだ確立されていないといえる。したがって、実船抵抗値の算定も、採用する各要素の計算法に対応して、実績の解析から求められた修正項を加味することによって行われる
1-1 摩擦抵抗式
(Frictional Resistance Formulae)
摩擦抵抗の計算は船体浸水表面積と同じ面積の平板に対するものとして扱われてきたが、理論の進歩と実船実績との対応から、使用される摩擦抵抗式そのものについての変遷もあり、また実船外板表面に対する粗度修正あるいは船体曲面の影響等を考慮した形状影響係数の導入等、他の抵抗要素の算定とも関連して、摩擦抵抗値もおのづから異なったものとなる。
摩擦抵抗は一般に
RF = CF・(1/2・ρ・S・ν^2)
で表わされる。ここに、 CF は摩擦抵抗係数で Reynolds 数の関数である。
以下に代表的な摩擦抵抗式を挙げる
(a) Froude の式
上記の一般式と異なるが、順序として、古くから用いられてきた Froude 式は、
RF = σ・λ{1 + 0.0043(15 - t)}・ S・ν^1.825, (kg) (5.2)
ここに、の:流体の比重
λ≒ 0.1392 + 0.258/(2.68 + Lw)
t: 流体の温度 (°C )
過去における相当期間、水槽試験資料は本式に基づいて整理されてきたが、摩擦抵抗は理論的には Reynolds 数の関数であるべきこと、また、この式が外板溶接の大型船に対し過大な値を与えること等、実船に延長して適用する場合,不具合な点があり、現在は使われることは少ない。
以下は式(5.1) 中の CFに対するものであるが、これらはいずれも滑面板 に対するもので実船に適用する場合は表面粗度の修正が必要である。
(b) Schoenherr の式
Schoenherr の摩擦抵抗係数を (CFS ) として、
0.242/√(CFS)=log10 (Rn・CFS) (5.3)
また、近似的に、
CFS ≒ 0.463・(log 10 ・R n )^ -2.6 (5.4)
本式は一応理論的に矛盾のないこと、また模型水槽試験の範囲では、この式による値は従来用いられてきた Froude 式による値とほとんど一致することなどから、これまで Froude 式で整理されてきた模型試験による剰余抵抗算定図表等がそのまま利用できる利点から、この式の用いられることが多い。
(c) ITTC (International Towing Tank Conference)
1957年式
本式の係数(CFI)は、
CFI=0.075/(log10・Rn-2)^2 (5.5)
この式は実船範囲では Schoenherr 式とほとんど変らない値を与え、模型船範囲で若干大きな値となるが、表現が簡単で使用し易い利点がある。
(d) Hughes の式
Hughes 式の係数(CPH)は、
CPH = CFHO・(1+K) (5.6)
で表わされ、CPHO は縦横比無限大の滑面平板に対するもので、
CFHO = (1.328・Rn^-0.5 + 0.014・Rn^-0.114)
Hughes は多数の曳航試験の結果から、外挿によってL/B→0のときの基準摩擦抵抗係数 CFHOを求めた。このCFHO値は
Schoenherr 値より低い。また、式(5・6) 中のKは形状影響係数で、造波抵抗がほとんど現われない低速における水槽試験の全抵抗係数と CFHOとの差を、流れが船体のごとき曲面に沿って流れる場合の摩擦抵抗の増加とみなし、この値を▽^(1/3)/L及びL/dに対する図表で与えている。
最近における造波抵抗理論の展開から、造波抵抗が単独に計算可能な域に達し、摩擦抵抗はK係数を考慮するのがより合理的であるとされている。現在,水槽試験の解析整理にはこの方法がとられている場合が多いが、設計初期段階での抵抗計算を全面的にこの方法に準じて行うには、対応する造波抵抗資 料の整備がいまだ必ずしも十分でない。
1-2 粗度修正係数(Roughness
Correction Factor)
模型水槽試験に基づく実船抵抗推定値と実船実績の解析より求めた抵抗値との差は、摩擦抵抗係数に対する修正量すなわち粗度修正係数(△CF)として扱われている。
抵抗計算に用いる摩擦抵抗係数は、一応、滑面板に対するものであるため、実船の外板粗度に対する修正は当然のものであるが、この△CFは結果的には抵抗各要素の算定方法あるいは実績解析過程における誤差等にもより直接影響される性格のもので、いわば計算馬力と実績馬力との間の調整項の意味をもつものといえる。
上述のごとく、△CFの値は、採用する摩擦抵抗係数値あるいは形状影響係数の考慮いかんによって変るものであるが、以下では摩擦抵抗係数として Schoenherr 式を用いるものとする。
全抵抗をRとし、従来の剰余抵抗 (RR) を用いるいわゆる2次元解析法の場合、その時の△CFを△CF2として、
R=(Cp+△CF2)1/2ρ・S・ν^2+Rn
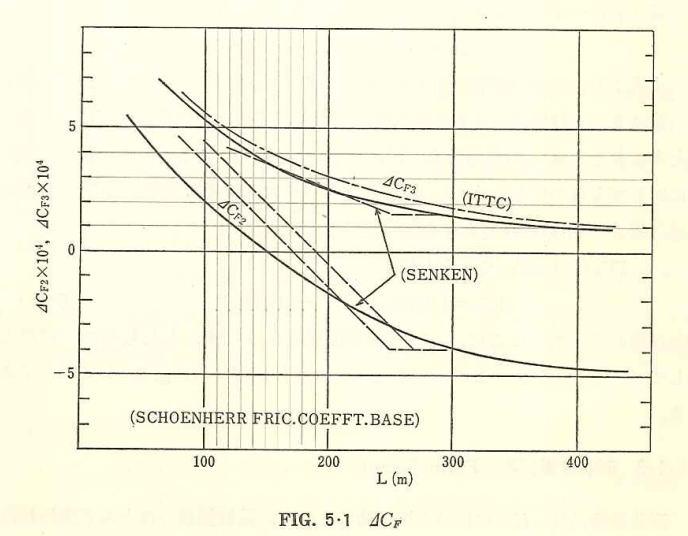
で、 △CF2の値は上述のごとき理由から、ある程度の分散があるが, 船長に対する平均的な値を(Fig. 5.1) に示してある ΔCF2 の値は船長(L)とともに減少し,150m程度以上で負の値となっている ΔCF2 の“船研” 標準値(横尾幸一,造船学会誌491号)も同図に示してある。
また、形状係数(K)と造波抵抗 (Rw) とを用いる3次元解析法の場合, このときのΔCFを ΔCF3として、
R={CF (1+K) + ΔCF3 }・1/2・ρ・S・ ν ^ 2
ここで、 CR を剰余抵抗係数, Cw を従来の模型試験による全抵抗から粘性抵抗を減じたいわゆる造波抵抗に対する抵抗係数とし、また CFM を模型船に対する摩擦抵抗係数とすれば、
RR = CR・ 1/2・ρ・S・ν ^ 2 (5 .9)
Rw = Cw・1/2・ρ・S・ν ^ 2 = (CR -K・CFM )・ 1/ 2・ρ・S・ν^ 2 (5 .9)
式 (5・7)~(5・9) より 、
ΔCF3 = ΔCF2 +K(CFM -CF )
本式より、従来の解析法による ΔCF2 から ΔCF3 が得られる。もちろん ΔCF3 の値は3次元解析法による水槽試験に基づき、実績との比較から直接求めることもできる。 ΔCF3 の概略値も (Fig. 5・1) 中に示してあるが、この値は大型船に対しても負の値となっていない。なおバラスト状態に対する ΔCF は満載状態の値より 0.0001程度大きくなっている。
ITTCは ΔCF3 の値として、
ΔCF3 = {105・ ( α / LW) ^ (1/3) - 0.64}・ 10 ^ - 3
を採用している。ここに、αは外板表面粗度をµで表わしたもので、基準としてα = 150 をとる。この場合の ΔCF3 の値も同様に (Fig. 5・1) に示してあ る。
1-3 形状影響係数(Form
Factor)
形状影響係数(K) は模型水槽試験において、造波抵抗のほとんど現われな
K=(RM-RFM)/RFM (5.12)
として求められる。
K値の近似推定式としては笹島教授等の式 (関西造協誌139号)があるが、この表現法を参考とし、主として“造船技術センター”での水槽試験資料から求めた、ほぼ、L/B>5, B/d<3, Cb>0.6の船型の満載状態に対するK値の近似値は, Schoenherr 摩擦係数に対し、
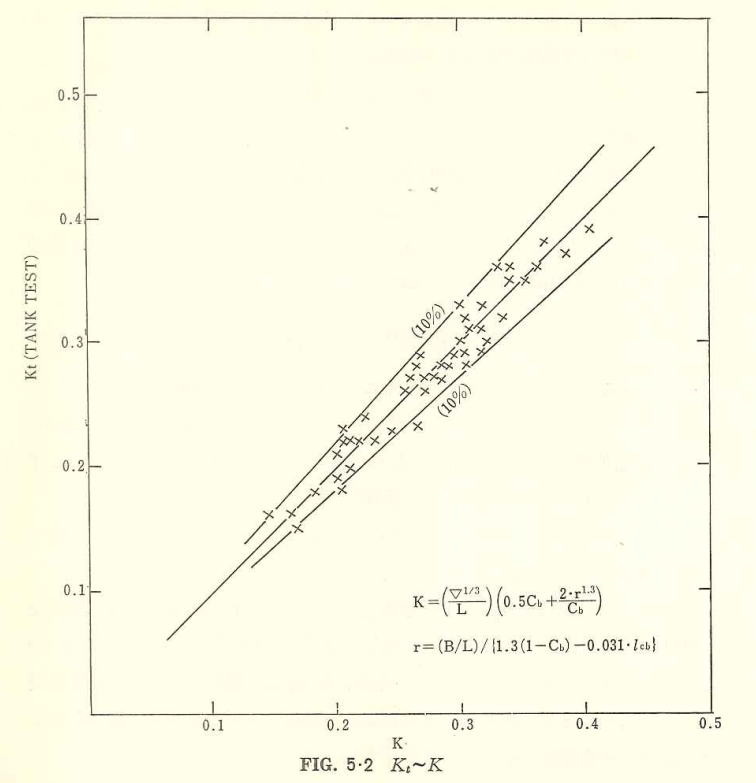
K≒(▽^(1/3)/L)・(0.5Cb + 2・γ^1.3/Cb) (5.13)
で与えられる。ここに、γは笹島教授による船尾肥大度を表わす係数で、
γ=(B/L)/{1.3(1-Cb)-0.031・ιcb} (5.14)
ιcbは浮心位置のミドシップからの距離のLに対する%で、ミドシップより前方を(一)とす る。またγはCbのみの関数として近似的に、
γ≒(B/L)/(0.91-0.73・Cb) (5.15)
で表わすことができる。
K値は抵抗計算において重要な要素となるため、式 (5・13) の算定精度を水槽試験値と比較し (Fig. 5・2) に示してある。同図でみるごとく式 (5・13)の誤差範囲は、ほぼ±10%である。なお、K値は、推定式に用いた船型主要素のみでなく、とくに船尾部の比較的微妙な変化によっても相当影響されることがあり、特異形状の場合は注意を要する。
また、バラスト状態でのK値 (KB)にも適用できる十分な推定式はいまのところみいだし難く, CbF=0.75~0.80近辺を境として, CbF 小なる場合は、KB値は満載状態の値より大となり, CbF 大なる場合は逆に小さくなる傾向がある。
KB値の大略の目安として、あえて表わせば、
K≒K{1+(3.52-4.4CbF) (1-ΔB/ΔF)}, CbF<0.80 (5.16)
≒K{1+(6.40-8.0CbF) (1-ΔB/ΔF)}, CbF>0.8 (5.16)
ここに、ΔB、ΔFはそれぞれバラスト状態及び満載状態排水量。
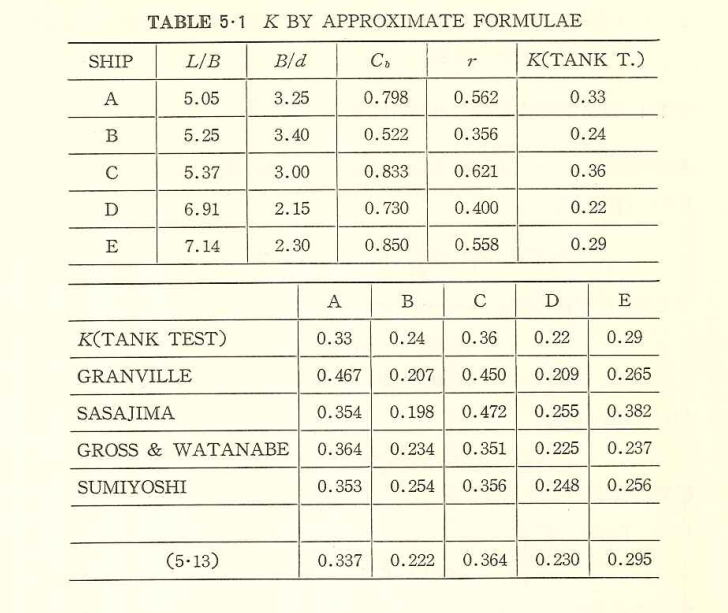
参考として次に他のK値推定式を挙げ、これらによる数船型についての比較例を(Table 5・1)に示す。
1) Granville 式
K=18.7(Cb・B/L)^2)
2) 笹島式(関西造協誌139号)
K=(3・γ^5 + 0.30)-0.035B/d+0.5・(t/L)・(B/d)
r:式(5.14), t: トリム、
3) Gross & Watanabe 式 (13th, ITTC, 1972)
K=0.017+20・Cb/(L/B)²√(B/d)
4) 住吉式(造船技術センター技報,No.2)
K=0.0905+15.1.Cb/(L/B)²√(B/d)
5) 多賀野式(関西造協誌146号)
肥大船型に対し,
K = -0.087+8.91 Cmid/(L/B・ √(((B/D)・Cb)・Cb))・B/Lγ
Lγ: 船体後半部のCF曲線を2次曲線と平行部分とにおきかえたときの 2次曲線部分の長さ。
1-4 浸水表面積
(Wetted Surface)
摩擦抵抗式中の浸水表面積 (S) の代表的な近似計算式は、
(a) Olsen 式
S=C・L・B (1.22・(d/B)+0.46) (Cb+0.765), (m²) (5.17)
ここで、C係数の値は、船体付加物を含むものとして、
C≒1.03 : 普通型船首
≒1.05 : 球状船首
(b) Denny式
S=C(1.7d+Cb•B)L=C(1.7・d+▽/d), (m²)
C係数値は (a) の Olsen 式とほぼ同じ。
(c) Taylor 式
S=C・√(▽・L) , (m²)
本式のC値はB/d, ▽/L^3及びCPによって決まるが、普通型船に対する近似値は2.67,球状船首の満載状態に対し2.72, 満載状態のほぼ50%以下のバラスト状態に対し2.98である。
なお、船体付加物の浸水面積 (Sa)の概略値は、単螺旋船に対し、
Sa≒1.5・L^0.8, (m²)
で表わされているが、上述のS値近似式はSaを含むものと考えてよい。また2軸船のSは1軸船の約2%大となる。
1-5 剰余抵抗と造波抵抗 (Residuary Resistance & Wave Resistance)
計画段階での馬力計算における剰余抵抗あるいは造波抵抗は系統的模型試験に基づく資料によるのが普通である。従来の資料は剰余抵抗を対象としたもので、代表的なものに Taylor 図表 (“Speed and Power”)と山県図表(“船型学”)がある。
Taylor 図表は
B/d=2.25, 3.75の場合に対し、V/√L、CP及びΔ/L^3から、単位排水量当りの剰余抵抗値を求め、 B/dの相違に対しては挿間法により求める。
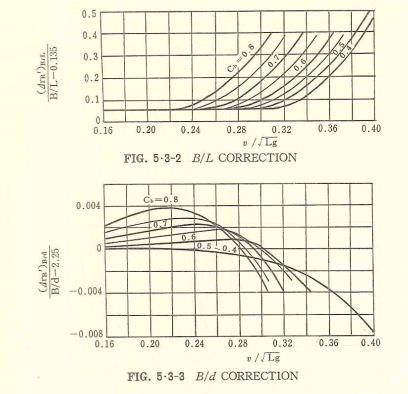
山県図表は、剰余抵抗を、
RR=γR'・1/2・ρ・▽^(2/3)・ν^2 (5.21)
γR'=kP・{γRO'+(ΔγR')^(B/L)+(ΔγR')^(B/4)} (5.21)
で表わし、B/L=0.135, B/d=2.25の基準船型に対する剰余抵抗係数(γRO'),及び B/L=, B/dが基準値と異なるときの修正量 (ΔγR')^(B/L), (ΔγR')^(B/d)を与えたものである。また、kPは1軸船で1.0, 2軸船で1.1~1.2の値とする。
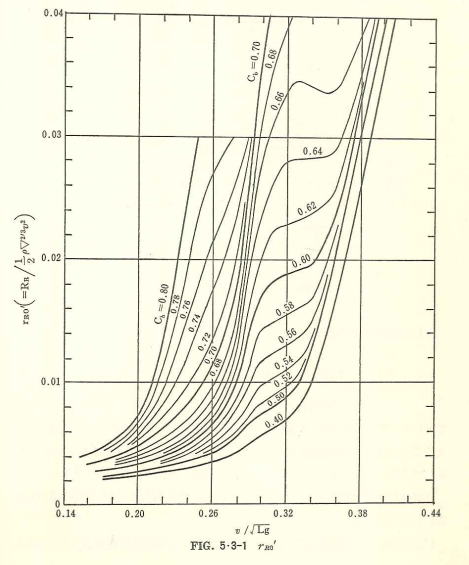
普通商船船型に対しては、山県図表が適当と考えられるので、 (Fig. 5.3)にこれを示してある。
以上ほのか、高速船型を対象としたものに、日本造船研究協会 SR45 部会
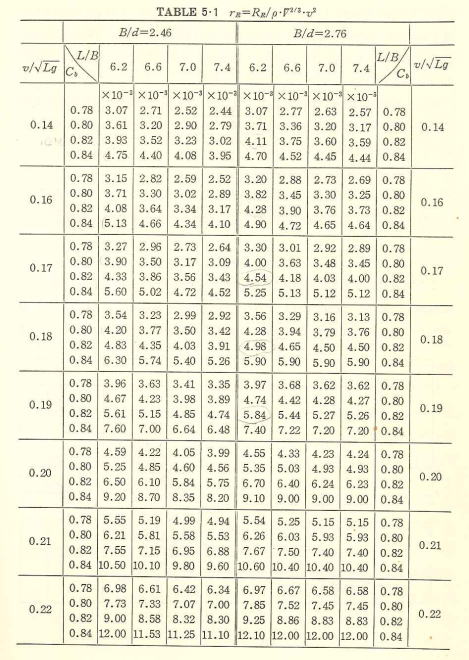
報告“Design Charts for the Propulsive Performance of High Speed Cargo Liners” (S39), またCが0.8前後の大型肥大船船型を対象とした船舶
技術研究所報告 1.6 (S39)がある。後者の満載状態に対するものを表形式にしたものが (Table 5.1)-(参考図書2)である。
なお、形状影響係数(K)に関連した3次元解析法に対応する造波抵抗係数の系統的に整理された図表はまだないが、剰余抵抗係数の算出資料が明確であれば、これから再解析して求めることができる。
すなわち、式 (5・9) の関係から、
CW=CR - K・CFM (5.22)
また、CR、CFM を造波抵抗の無視できる低速での値とすれば、K=CR/CPMで、
CW=CR - (CR/CFM) ・CFM (5.23)
この関係に基づき(Table 5.1) の剰余抵抗係数(γR)を造波抵抗係数(γw)に換算したものが(Fig. 5・4)である。(Fig. 5・4)をみると、原資料のL/B=6.2~7.4の範囲ではL/Bによるγwの変化はほとんど現われておらず,結
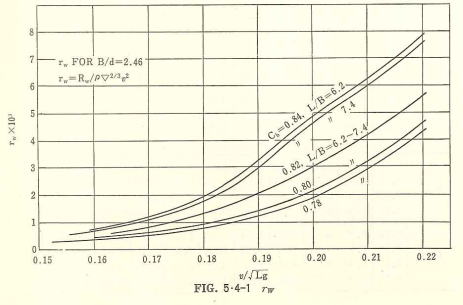
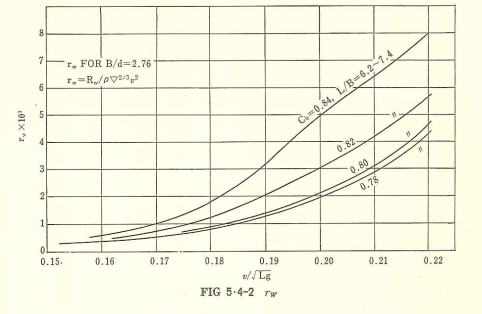
果として L/B の影響はK係数に吸収された形となっている。なお、(Fig. 5.4-1)及び(Fig. 5・4-2)は、それぞれB/d=2.46, 2.76に対するものであるが, B/d のこの程度の差による相違は上記両図からは明瞭でない。
上述の図表による抵抗計算の主要素は、主要寸法のほかにv/√(Lg) 及び Cbであるが,厳密には他の船型要素によっても当然影響をうけ、例えば、最近の抵抗理論を適用した最適化プリズマ曲線等により、船型によっては、造波抵抗の数十%程度の減少も可能とされている。
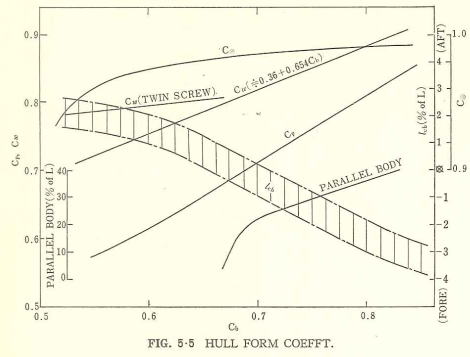
普通、Cbはν/√(Lg) に対して (Fig. 2・2) に示したごとき範囲で選定されるが、Cbに対する他の船型要素を (Fig. 5.5)の基準値に近くとるとき,抵抗自体に対する影響はそれ程大きくなく、実用的には従来の図表をまずそのまま利用しても差支えないであろう。なお, (Fig. 5・5) に示した船型要素諸数値のうち, Lcb の変化は抵抗値に対して比較的影響を与えるものであるが,高速船型資料の一例では、Lcbの最適値からの±0.4の差は剰余抵抗の約2%の増大となる程度である。
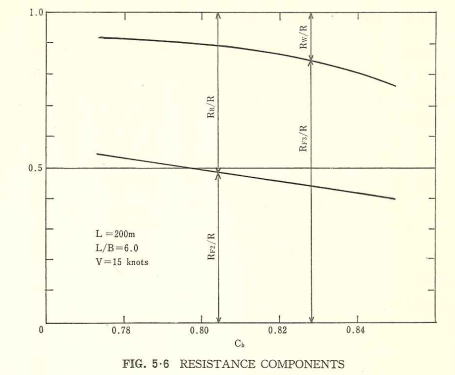
なお、(Fig. 5・6)には200m級タンカーの場合の、2次元解析法による剰余抵抗(RR)と3次元解析法による造波抵抗
(Rw)の全抵抗(R)に対する割合を示してあるが、船型の大型化とともにRw/Rはさらに小さくなり,300m級ではこの割合はほぼ半減する。いずれにしてもRw/Rは従来のRR/Rに較べ相当小さな値となっており、とくに大型専用船の抵抗計算における造波抵抗値の重点度は比較的小さなものであるといってよいであろう。
造波抵抗計算については、近年,乾教授をはじめとする理論的展開がめざましく、とくに大型球状船首は現在広く採用されている。
造波抵抗理論の実際船型への適用には、電算機による高度の計算も必要とするが、球状船首についても、その普通型船首と較べての効果を精度ある具体的数値で表現することはなお困難な段階にある。
本節では剩余・造波抵抗係数は普通型船首に基づくものを挙げてあるが、関
連する形状係数は主として球状船首船型の資料から求めたものであり、これらの値を用いての全抵抗値は若干大きめの値を与える場合もあると思われるが実用上はとくに支障のない程度のものである。
以上の過程によって得られる各抵抗要素の和がいわゆる裸殼全抵抗で、単螺旋船に対してこれをそのまま採って差支えないが、双螺旋船に対しては、十分な資料に欠けるが、概略次の如き数値を付加物抵抗として裸殼全抵抗に加算する。
双螺旋ボッシング 3~7%
'A' 型ブラケット 5~10%
バウスラスター 2~5%
1-6 空気抵抗(Air
Resistance)
普通船舶での通常試運転時の空気抵抗は水抵抗と比較して無視できる程度の ものであり、計画段階での馬力推定では粗度修正係数等の計算・計測誤差集約
項に含めて扱われているが特殊の場合についてはこれを考慮する。
空気抵抗 (RA) は、
RA = ka・ 1/2・ρa・A・νw ^ 2
で表わされ、ここに、
pa:空気密度, 15 deg
* C において0.124 (kg・ sec^ 2 / (m ^ 4) )
A : 船の水線上前面面積, (m
^ 2)
V :相対風速 ( m /sec)
ka:抵抗係数で、概略値は、 ≒ 1.25sin(1.5α+ 45°)
a :船首方向に対する風向角度, (deg.)